EIGamal加密算法

背景介绍

DH(Diffie-Hellman)算法

DH算法用于在不安全的公共通道中协商密钥，安全性体现在：在有限域上计算离散代数非常困难。上两位大牛Whitfield Diffie 和 Martin Hellman的照片：

算法描述：

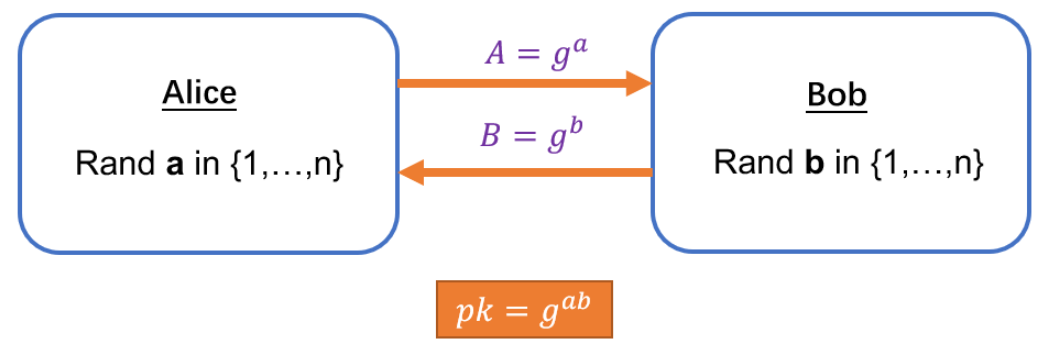
假定Alice和Bob期望在一个不安全的网络中协商一个共同的密钥，那么进行如下步骤：

• 两人先说好大素数（质数）p和它的原始根g。
• Alice随机产生一个数a，并计算\(y_A = g^a \mod p\), 发送给Bob。
• Bob随机产生一个数b，并计算\(y_B= g^b \mod p\)，发送给Alice。

此时， Alice手握Bob发过来的\(y_B\)，结合自己产生的a，开始这样计算：

\(y_B^a \mod p = (g^b \mod p)^a \mod p = g^{ab} \mod p\)。

Bob也拿到了Alice发来的\(y_A\)，同时结合自己的b，也开始计算：

\(y_A^b \mod p = (g^a \mod p)^b \mod p = g^{ab} \mod g\)。

这样Alice和Bob都得到了相同的密钥。

EIGamal诞生

ElGamal算法是由Tather ElGamal在1985年提出的，它是一种基于离散对数难题的加密体系，与RAS算法一样，既能用于数据加密，也能用于数字签名。ElGamal算法是基于因数分解，而ElGamal算法是基于离散对数问题。与RSA算法相比，ElGamal算法哪怕是使用相同的私钥，对相同的明文进行加密，每次加密后得到的签名也各不相同，有效的防止了网络中可能出现的重放攻击。

• 原文的链接：[A public key cryptosystem and a signature scheme based on discrete logarithms](https://ieeexplore.ieee.org/abstract/document/1057074/)

这篇论文在谷歌学术上被引用了将近10000次，可以说有想当广泛的影响力，大家如果有时间可以欣赏一下作者是怎么行文的，EIGamal加密算法十分的简单，看看作者是如何将其扩充到9页，也是一种锻炼自己的方式嘿嘿。

基于离散对数的数学难题

基本描述

如果对于一个整数y和质数p的一个原根g，可以找到一个唯一的指数x，使得：

$y=g^x $其中 \(0≤x≤p−2\)成立，那么指数x称为y的以g为基数的模p的离散对数。

离散对数难题是指：当已知一个大质数p和它的一个原根g，如果给定一个y，要计算x的值是相当困难的。

针对不合理参数的破解方法

当质数满足\(p = 2^n+1\)

当\(p = 2^n+1\),x可以被转化成二进制序列\(\{b_0,\dots,b_{n-1}\}\),其中\(b_i\in \{0,1\}\),有如下等式 \[ x = \sum_{i=0}^{n-1}{b_i*2^i} \] 注意到，因为g是模数p的一个原根，所以集合\(\{g^i|i\in[0,p-2]\}=\{1,\dots,p-1\}\),两个集合即两个集合应该相等，由Euler小定理: \[ g^{p-1} \equiv 1 \pmod{p} \] 那么对方程开方: \[ g^{(p-1)/2} \equiv -1 \pmod{p} \] 为什么不是等于1呢，因为已经有\(g^0=1\)了，\(g^{(p-1)/2}\)不能和\(g^0\)相等（集合\(\{g^i|i\in[0,p-2]\}\)等于素数p的既约剩余系），所以只能等于-1

有了上面的基础，我们可以简单推导出下面的公式 \[ y^{(p-1)/2} \equiv (g^x)^{(p-1)/2} \equiv (-1)^x \pmod{p} \] 根据x的二进制序列，当x的最低位

• \(b_0=0\)时，\(y^{(p-1)/2} \equiv 1 \pmod{p}\)
• \(b_0=1\)时，\(y^{(p-1)/2} \equiv -1 \pmod{p}\)

由此我们可以确定第一位\(b_0\)的值，我们继续令\(z \equiv y*g^{(-b_0)}\equiv g^{x_1} \pmod{p}\),这里 \[ x_1 = \sum_{i=1}^{n-1}b_i*2^i \] 如果\(b_1=0\)那么\(x_1\)是4的倍数而不是2的倍数，有下面的等式 \[ z^{(p-1)/4} \pmod{p} \equiv \begin{equation} \begin{cases} +1,b_1=0\\ -1,b_0=1 \end{cases} \end{equation} \] 由此我们有可以判断一位\(b_1\)，以此类推，我们可以完全复原密文x

当p没有大素数因子

EIGamal流程介绍

密钥产生

• 选取一个强素数\(p\)，而且满足\(p-1\)至少有一个很大的质因数（如果因子很小那么计算离散对数很简单）
• 素数\(p\)的一个本原根\(g\)
• 随机选取整数\(a\)

产生一个公钥\(pk = (p,g,g^a)\)，私钥是随机选取的整数a

加密

假设Alice想发送一个密文m给Bob

• 随机选取一个数\(k\in[1,p-2]\)
• 计算\(c_1 = g^k \mod p\)
• 再计算\(c_2 = (g^a)^k*m \mod p\)

如此就计算出了密文，这是一对数\((c_1,c_2)\)，并将其发送给Bob

解密

Bob讲密文恢复成明文m

• 计算\(v \equiv c_1^a \pmod{p}\)
• 计算\(m \equiv c_2*v^{-1} \pmod{p}\)

证明：

\(m \equiv c_2*v^{-1} \pmod{p} \equiv m*g^{ak}*(g^{ak})^{-1} \pmod{p} \equiv m \pmod{p}\)

python程序实现

参数生成

强素数满足p-1至少有一个大因子，可以用Crypto.Util.number里的函数getStrongPrime()，这样可以直接产生一个非常强的素数。但是这样有几个问题：

• 这个函数随机生成的强素数的bit位数必须是128的倍数而且大于512。一方面导致了计算时间的增大，令一方面如果p太大可能导致不安全（比如\(g^a \mod p\)可能在数值上就等于\(g^a\)，而有些同学喜欢默认为原根就是2,3,5中的几个，如果a取的不是很大，我们可以直接开方，如果是整数那么这个就是我们要的a）
• 这个素数因为有大因子，在验证g是原根的时候，这几个大因子寻找十分困难，以至于时间很长很长

下面给出一个解决方案：

我们只需要p-1有一个大因子就行了，我们默认大因子为素数q和数字2，这样就有关系p = 2*q+1,如此一来，我们只需要验证p-1的两个因子即可判断是不是原根

def Gen_primitive_root(p,q):
    #产生一个本原根，产生方法，从2，3，... ，p-1逐个选取
    #选到2的时候，选取phi(p)的几个非1因子，比如phi(11)=10,10有因子2，5
    #如果2的2次方和5次方都不等于1，那么一定2的10次方等于1，这时候2为本原根
    #但，这样真的很慢很慢

    while True:
        candidate_root = random.randint(2,p-2)
        #按照Gen_para生成的素数p只有两个素因子2和q
        if gmpy2.powmod(candidate_root,2,p)!=1 and  gmpy2.powmod(candidate_root,q,p)!=1:
            return candidate_root     
        
def Gen_para(m):
    digit = len(str(m))
    while True:
        #这里是一个坑，尽量吧q的范围扩大一点，这样有更大的几率让2*q+1是一个素数
        q = sympy.randprime(10**digit, 10**(digit+1))
        p = 2 * q + 1
        if sympy.isprime(q):
            if  gmpy2.is_prime(p):
                break
    g = Gen_primitive_root(p,q)
    a = random.randint(2 , p-2)
    return [p,g,pow(g,a,p)],a

加解密实现

参数生成了之后加解密就没什么好说的了

def encrypt(m,pk):
    k = random.randint(1,p-2)
    print("参数k的值为:%d"%k)
    c1 = pow(g,k,p)
    c2 = (pow(g_a,k,p) * m)%p
    return  c1,c2 

def decrypt(c1,c2,sk):
    v = pow(c1,sk,p)
    m = c2*sympy.invert(v,p) % p
    return m

完整代码

import random
import gmpy2
import sympy

def Gen_primitive_root(p,q):
    #产生一个本原根，产生方法，从2，3，... ，p-1逐个选取
    #选到2的时候，选取phi(p)的几个非1因子，比如phi(11)=10,10有因子2，5
    #如果2的2次方和5次方都不等于1，那么一定2的10次方等于1，这时候2为本原根
    #但，这样真的很慢很慢

    while True:
        candidate_root = random.randint(2,p-2)
        #按照Gen_para生成的素数p只有两个素因子2和q
        if gmpy2.powmod(candidate_root,2,p)!=1 and  gmpy2.powmod(candidate_root,q,p)!=1:
            return candidate_root          

def Gen_para(m):
    digit = len(str(m))
    while True:
        #这里是一个坑，尽量吧q的范围扩大一点，这样有更大的几率让2*q+1是一个素数
        q = sympy.randprime(10**digit, 10**(digit+1))
        p = 2 * q + 1
        if sympy.isprime(q):
            if  gmpy2.is_prime(p):
                break
    g = Gen_primitive_root(p,q)
    a = random.randint(2 , p-2)
    return [p,g,pow(g,a,p)],a

def encrypt(m,pk):
    k = random.randint(1,p-2)
    print("参数k的值为:%d"%k)
    c1 = pow(g,k,p)
    c2 = (pow(g_a,k,p) * m)%p
    return  c1,c2 

def decrypt(c1,c2,sk):
    v = pow(c1,sk,p)
    m = c2*sympy.invert(v,p) % p
    return m


if __name__ == "__main__":
    file_name = "secret0.txt"
    f = open(file_name)
    m = int(f.readline())
    pk , sk = Gen_para(m)
    p,g,g_a = pk
    print("素数p为%d"%p)
    print("原根g为%d"%g)
    print("参数g^a为%d"%g_a)
    c1 , c2 = encrypt(m,pk)
    print("密文c1为%d"%c1)
    print("密文c2为%d"%c2)
    m_d = decrypt(c1,c2,sk)
    if m == m_d:
        print("解密正确")